JPEG 的实现原理
内容过时
本文源自 https://sixplain.com/2020/11/08/jpeg/
源网站无法访问,故备份于此
JPEG 是一种常见的图像压缩格式,它采用的是有损压缩技术,也就是为了让体积变小,丢掉了一部分图像信息。下面就来看下 JPEG 的实现原理。
图像显示
在了解 JPEG 的实现原理前,我们先来看下图像是如何显示的。计算机最常用的色彩空间是RGB(红绿蓝三原色),屏幕上每一个像素都是由红绿蓝三个颜色通道叠加最终显示出来。
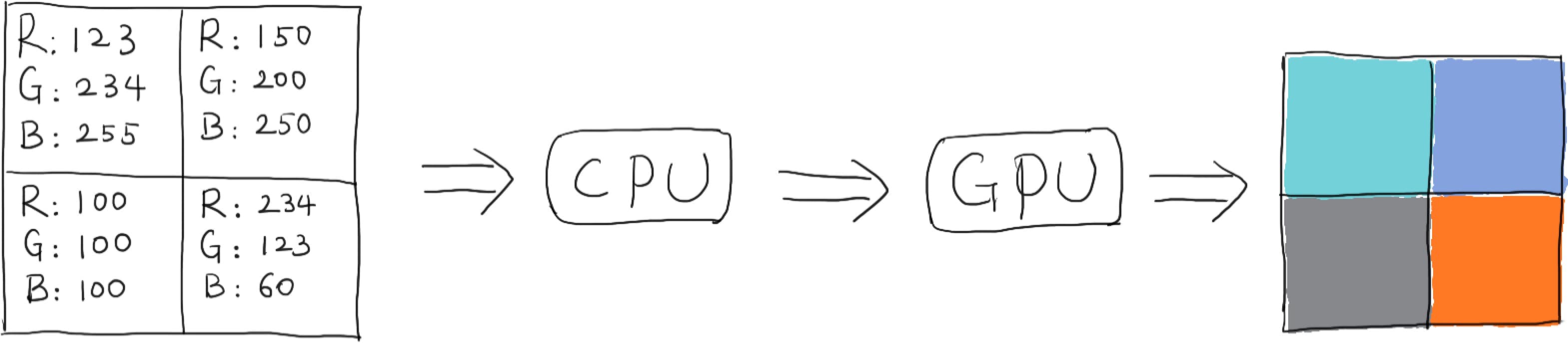
RGB 虽然是计算机最常用的色彩空间,能够直接对应显示器的显示。但是对于数据传输而言,RGB色彩空间并不合适。于是就有了各种图片编解码格式,不同的图片格式,在解码之前会有各自的压缩方式,有的是无损压缩,有的是有损压缩,存储的格式也是各不相同:

对于 JPEG 来说,它的主要过程是:
- 把数据分成「重要部分」和「不重要部分」
- 滤掉不重要部分 [[3]]. 将剩下重要的数据进行压缩存储
色彩空间转换 (Color Space Convert)
这个词初听起来有点奇怪,色彩怎么还有空间,空间怎么还能转换?这里所说的色彩空间其实就是对颜色的不同表示方式。比如「红色」,可以从红黄蓝三原色的角度去描述,也可以从色相饱和度的角度去描述

JPEG 在编码时充分考虑了人眼的特性:相对颜色而言,眼睛对亮度更加敏感(因为有更多的视杆细胞)。所以可以将颜色用亮度结合色度的方式来表示: YUV
Y 表示明亮度(Luminance), U 和 V 分别表示色度(Chrominance)和浓度(Chroma)。
和 RGB 类似,每个像素点都包含 Y、U、V 分量,但 Y 和 UV 是可以分离的,只有 Y 也可以显示完整的图像,只不过是黑白的。
YUV/YCbCr 是一种电视信号传输所用的色彩空间,对应一个亮度通道 Y 和两个色差通道 Cb 和 Cr。早期只有黑白电视,所以电视信号只需要 Y 通道即可。后面出现了彩色电视,就加上 CbCr 这两个色差信号,而原本的黑白电视只需要处理 Y 通道即可,能够兼容黑白彩色电视的信号传输。
取样 (Downsampling)
既然眼睛对亮度更敏感,且已经分离出了亮度和色度,那是不是可以去掉一些色度信息来节省空间呢,这就是「取样」做的事情:压缩 UV 值。比如 4:2:2 采样,它的含义是每 4 个 Y 采样点,有 2 个 U 和 2 个 V。也就是 UV 分量是 Y 分量采样的一半,假设 Y 分量用 X 表示,U 分量用黑圈表示,V 分量用红圈表示

假如图像像素为:[Y0 U0 V0]、[Y1 U1 V1]、[Y2 U2 V2]、[Y3 U3 V3]
那么采样的码流为:Y0 U0 Y1 V1 Y2 U2 Y3 V3
其中,每采样过一个像素点,都会采样其 Y 分量,而 U、V 分量就会间隔一个采集一个。
最后映射出的像素点为 [Y0 U0 V1]、[Y1 U0 V1]、[Y2 U2 V3]、[Y3 U2 V3]
这样原先 12 个单位的信息量,经过 4:2:2 采样后,只需存储 8 个单位的信息量,减少了 1/[[3]] 的体积。如果是 4:1:1 的话,则可以减少 50% 的体积。

分块
分块的过程是把图像以 8 x 8 的大小分成多份,方便后续的矩阵操作。以 Lena 的 Y 分量(明度)为例:

如果不能被 8 整除,会在图像的右边和底部增加额外的像素(因为矩阵操作对元素的数量有要求)。
离散余弦变换 (DCT)
这是 JPEG 压缩算法的核心,这个变换的目的是将数据从空间域转换为频域,再结合眼睛对高频不敏感的特点,将高频数据去除。什么叫「从空间域转为频域」?这就要请出傅立叶老师了,傅立叶发现看似复杂的周期函数,其实可以用一系列简单的正弦、余弦波之和来表示,比如下面这个看起来有点奇怪的函数:

它可以由多个不同频率/振幅的正弦/余弦波组成

从正面(时域)看,这个波一直在动,但从侧面(频域)看,它其实就是几根线

那这跟我们要做的事情有什么关系呢?假设 Y 分量是一维数据,只有 X 方向的值:
[100, 50, 25, 75, 100, 0, 125, 200]
将它们转换为坐标,看起来就像这样:

可以将它构造为某个周期函数的一部分,就像这样:

你看,有了一条函数曲线,就可以将它转换为不同频率的正/余弦组成的结果,这就完成了时域转到频域的转换。但这里有 x,y 二维数据,又该如何做呢,那就把坐标系拓展成三维,看起来像是这样:

是不是很像一座座小山,如果把山谷用黑色标记,山峰用白色标记,就会得到这样的效果:

黑白交错地越密,频率越高。接下来该有请主角离散余弦变换(DCT)上场了。它是离散傅立叶变换的精简版(去掉了虚数部分),方程式如下:

不要被它吓到,我们只需知道:每一个变换后的结果 D(i, j) (第 i 行,第 j 列元素),都跟原矩阵中的每一个元素与余弦函数的乘积有关。又因为我们只有 8 x 8 个元素,所以公式又可以精简为:

因为是离散函数,所以它的展示结果是这样的:

还是按照上面俯视的方式来看,山峰为白,山谷为黑,那么它对应的频率表(64 个 余弦函数)就像这样:

对于图像的 8 x 8 数据,可以通过这 64 个 cos 函数乘以对应的系数(coefficient)来表示。 系数越大表示该余弦函数对于图像数据的作用越大。
同时注意到频率从左上角到右下角依次递增,这对于下一步要做的「量化」很重要。
现在假设有一个 Y 分量的 8 x 8 block 数据如下:

因为明度的数据是从 0 - 255,但余弦函数需要数值在 -128 到 127 之间,所以需要先减去 128

接下来就要计算系数了,这里会进行矩阵运算。用乘法简单类比的话,就是已知公式 z = x·y,且已知 z 和 y 的值,求 x。这里的 z 是 Y 分量的明度值(减了 128 之后),y 是 频率表对应的矩阵,x 最终的计算结果为:

这里每一个位置的值,分别表示该位置上的余弦函数对应的系数,值越大,表示该余弦函数对结果的作用越大。
可以看到,左上角区域的值普遍大于右下角的值,这表示低频的贡献度比高频的大,在下一步的量化过程里,就可以对这些高频数值下手了。
左上角第一个数是个定值,所以也被称为 DC (直流分量),是整个矩阵的平均值。剩下的 63 个数被称为 AC(交流分量),越往右下角频率越高。
量化(Quantization)
JPEG 的质量控制(如 50%, 75% 等)就是发生在量化阶段。量化是对经过 DCT 变换后的低频高频分量进行处理,略去不重要的部分。因为眼睛对高频的敏感度弱于低频,因此可以舍去部分高频数据。怎么舍呢,这就涉及到「标准量化表」,明度标准量化表(Q50,也就是 50% 的质量)是这样的:

为什么说它是「标准量化表」呢,因为更高或更低的质量都可以由这个表计算而来,对于质量高于 50% 的可以用 (100 - quality level)/50 的方式来算,低于 50% 的直接 50/qulity level,比如 10% 质量的表:

对于上一步 DCT 得到的结果,我们将它应用标准量化表(每一个数除以量化表里对应位置的数,对小数结果四舍五入),可以得到如下结果:

那些人眼不太敏感的高频数据已经被清零了。压缩质量越低,量化表的值就越大,最终结果出现的 0 就越多,也就是被丢弃的信息越多。
压缩
得到量化后的矩阵就要开始编码过程了,首先要把二维矩阵变为一维数组,这里采用了 zigzag 排列,将相似频率组在一起:

先对直流分量 DC 进行差分编码(因为相邻图像块的 DC 差别不大,只要保留第一个图像块的 DC 和以后每一个 DC 之间的差值即可)。
再对交流分量 AC 进行游程编码,避免连续重复的数据。
一组资料串"AAAABBBCCDEEEE”,由4个A、3个B、2个C、1个D、4个E组成,经过游程编码可将资料压缩为4A3B2C1D4E。在这里就是(1,4),(1,3)…(3,0)…(2,-1),BOE。BOE 表示这个位置之后全都是 0
最后再使用哈夫曼编码对结果进一步无损压缩,至此 JPEG 的压缩流程就完成了。
这里还会涉及到 JPEG 内置的一些标准编码表用于信息的压缩和解压缩,就不展开讲了。

解压
解压的过程,先是将数据还原为量化后的 8 x 8 图像块,然后根据图像质量,计算量化表,得到 DCT 后的表格,再与 64 个余弦函数(实际运算中是两个矩阵的操作)运算得到被离散余弦函数转换前的数据,一路逆运算,最终得到图像的 RGB 信息。
延伸
由于 JPEG 压缩算法本身的问题,又衍生出了一些替代品,如可以实现渐进式加载效果的 Progressive JPEG(先展示模糊的内容,再逐步展示细节,但并没有减少文件尺寸,同时还增加了处理复杂度),可以实现无损压缩的 JPEG2000(这个用得比较少,有无损需求的通常会考虑 png / webp),完全兼容 JPEG API / ABI,同时能够实现更小尺寸的 mozjpeg(内部使用了 libjpeg-turbo),我自己使用下来效果还不错,可以看下这篇 webp 和 mozjpeg 的对比文章。
小结
JPEG 的压缩思路还是挺值得学习的,充分考虑使用者的特点(亮度优于色度,低频优于高频),用到了分治的思想,有损和无损压缩的结合,数学公式的使用等。虽然 20 多年前就在使用,且有了更多的图像格式选择,但依然是图片存储领域重要的一份子。